目录
本节介绍一些例子.
LASSO
考虑如下问题:
\[ \min \quad (1/2)\|Ax-b\|_2^2 + \gamma\|x\|_1, \] 其中\(x \in \mathbb{R}^n, A \in \mathbb{R}^{m\times n }\).proximal gradient method
proximal gradient method 是：
\[ x^{k+1} := \mathbf{prox}_{\lambda g}(x^k - \lambda \nabla f(x^k)) \] 令\(f(x)=(1/2)\|Ax-b\|_2^2, g(x)=\gamma \|x\|_1\), 则\[ \nabla f(x) = A^T(Ax-b), \quad \mathbf{prox}_{\gamma g}(x)=S_{\gamma}(x), \] 其中\(S_{\gamma}(x)\)是.ADMM
很自然的方法，不提了.
矩阵分解
一般的矩阵分解问题如下:
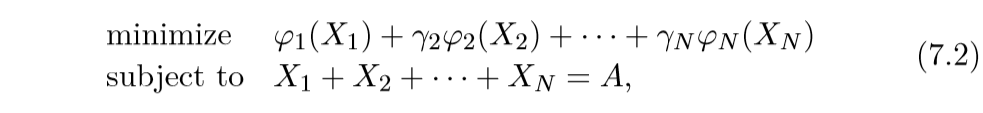其中\(X_1, \ldots, X_N \in \mathbb{R}^{m\times n}\)为变量，而\(A \in \mathbb{R}^{m\times n }\)为数据矩阵. 不同的惩罚项\(\varphi\)会带来不同的效果. - \(\varphi(X)=\|X\|_F^2\), 这时，矩阵元素往往都比较接近且小
- \(\varphi(X)=\|X\|_1\), 这会导致稀疏化
- \(\varphi(X) = \sum_j \|x_j\|_2\), 其中\(x_j\)是\(X\)的第\(j\)列, 这会导致列稀疏?
其他的看文章吧.
ADMM算法
令
\[ f(x) = \sum_{i=1}^N \varphi_i (X_i), \quad g(X)=I_{\mathcal{C}}(X), \] 其中\(X = (X_1, \ldots, X_N)\), 并且：\[ \mathcal{C} = \{(X_1, \ldots, X_N| X_1 + \ldots + X_N=A\}. \]根据之前的分析，容易知道:
\[ \Pi_{\mathcal{C}}=(X_1, \ldots, X_N)-\bar{X}+(1/N)A, \] 其中\(\bar{X}\)是\(X_1, \ldots, X_N\)的各元素的平均. 最后算法总结为：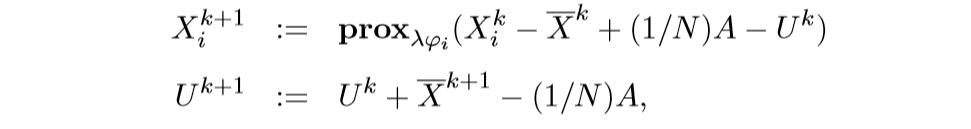
多时期股票交易
其问题是:
\[ \min \quad \sum_{t=1}^T f_t(x_t) + \sum_{t=1}^T g_t (x_t - x_{t-1}), \] 其中\(x_t, t=1,\ldots, T\)表示第\(t\)个时期所保持的股份，期权，而\(f_t\)则表示对应的风险，\(g_t\)表示第\(t\)个时期交易所需要耗费的资源.考虑如下分割:
\[ f(X)=\sum_{t=1}^ Tf_t(x_t), \quad g(X)=\sum_{t=1}^T g_t(x_t-x_{t-1}), \] 其中\(X=[x_1, \ldots, x_T]\in\mathbb{R}^{n \times T}\).随机最优
为如下问题:
\[ \min \quad \sum_{k=1}^K \pi_k f^{(k)} (x), \] 其中\(\pi \in \mathbb{R}_+^K\)是一个概率分布，满足\(1^T\pi=1\).利用第5节的知识，将此问题化为:
\[ \min \quad \sum_{k=1}^K \pi_k f^{(k)} (x^{(k)}) \\ s.t. \quad x^{(1)}=\ldots=x^{(K)}. \] 再利用ADMM就可以了.Robust and risk-averse optimization
鲁棒最优，特别的, 最小化最大风险:
\[ \min \quad \max_{k=1, \ldots, K} f^{(k)}(x). \] 更一般的:\[ \min \quad \varphi(f^{(1)}, \ldots, f^{(K)}(x)), \] 其中\(\varphi\)为非降凸函数.method
将上面的问题转化为:
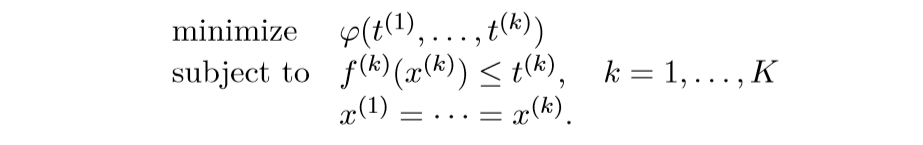
将
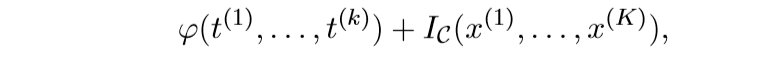视作\(f\) 而
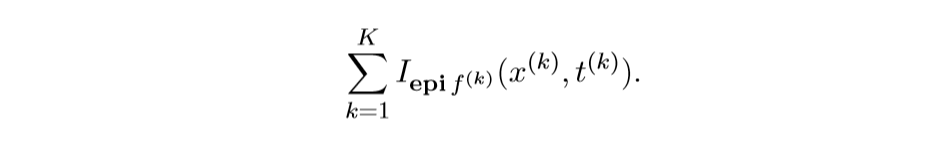作为\(g\)，再利用ADMM求解即可.